Исследовательская работа 7 класс Числа-палиндромы

Управление образованием Администрации

города Шарыпово Красноярского края

МУНИЦИПАЛЬНЫЙ ЭТАП КРАЕВОГО МОЛОДЕЖНОГО ФОРУМА

«НАУЧНО-ТЕХНИЧЕСКИЙ ПОТЕНЦИАЛ СИБИРИ»

МУНИЦИПАЛЬНАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ «ПЕРВЫЕ ШАГИ В НАУКУ»

«Числа-палиндромы»

С условиями Конкурса ознакомлен(-а) и согласен(-а). Организатор конкурса оставляет за собой право использовать конкурсные работы в некоммерческих целях и без денежного вознаграждения автора (авторского коллектива) при проведении просветительских кампаний, а также полное или частичное использование в методических, информационных, учебных и иных целях в соответствии с действующим законодательством РФ.

Шарыпово, 2018

Тезисы работы

Актуальность: Использование математики, в связи с научно-техническим прогрессом, на фоне всеобщей информатизации, имеет большое значение. У нас в классе многим нравится этот предмет. Но некоторые ребята опасаются трудных задач, больших вычислений. Может быть, они не любят математику? Или не понимают, зачем она нужна? Мне захотелось им помочь, раскрыть им глаза, научить любить эту науку, показать важность математики. Данная тема расширяет знания, кругозор, помогает при решении олимпиадных задач и задач для подготовки к экзамену.

Гипотеза: Если интересная информация о палиндромах, заинтересует школьников, то возможно они будут более углубленно изучать математику, что скажется на их математической грамотности и результативности обучения.

Цель: исследование палиндромов, репьюнитов, репдилжитов, выявление их особенностей и демонстрация возможности их использования на уроках математики и других предметов, расширение кругозора учащихся.

Знакомство с палиндромами.

Палиндро́м (от греч. πάλιν — ≪назад, снова≫ и греч. δρoμος—≪бег≫)

буквосочетание, слово или текст, одинаково читающиеся в обоих направлениях.

Я узнала, как можно получить такое число-перевёртыш:

Возьми любое число 619; Переверни его 916

Сложи два числа 1535; Переверни сумму 5351

Сложи два полученных числа 6886 Результат перевёртыш!

Палиндромы на самом деле очень увлекательны, они помогают развивать интерес к познавательной деятельности. Я узнала, что палиндромы, это не только интересные картинки в изобразительном искусстве и окружающем мире, но и числа в математике, слова и фразы в русском языке. Мой кругозор стал шире, я узнала много интересной и полезной информации.

Я думаю, что моё исследование поможет улучшить память, мышление, воображение.

Список литературы:

1. http://www.nkj.ru/archive/articles/17984/ (Наука и жизнь№5,2010г).

2. Кацюба Е.А.Первый палиндромический словарь.— Москва, 1999.

3. Е.А.Новый палиндромический словарь.— Москва, 2002.

4. Федин С.Н. Палиндроматика // Математика для школьников. – 2005. — № 1, с. 54.

5. Кордемский Б.А. Удивительный мир чисел // книга для учащихся. – М.: Просвещение, 1995.

6. Кордемский Б. А.  На часок к семейке репьюнитов // Квант. -1997. — № 5. — с. 28-29.

7. Перельман Я.И. Занимательная математика // издательство «Тезис». – 1994

8. http://arbuz.uz/t_numbers.html

9. Журнал квант

Я ничего не понимала в математике, поэтому мне пришлось думать. (Джоан Робинсон)

Не так давно я бороздила просторы Интернета и наткнулась на выражение «числа Шахерезады». Мне стало интересно, что это за числа, и я захотела узнать о них побольше.

Актуальность: Использование математики, в связи с научно-техническим прогрессом, на фоне всеобщей информатизации, имеет большое значение. У нас в классе многим нравится этот предмет. Но некоторые ребята опасаются трудных задач, больших вычислений. Может быть, они не любят математику? Или не понимают, зачем она нужна? Мне захотелось им помочь, раскрыть им глаза, научить любить эту науку, показать важность математики. Данная тема расширяет знания, кругозор, помогает при решении олимпиадных задач и задач для подготовки к экзамену.[5] Числа палиндромы образуют одно из наиболее интересных подмножеств множества натуральных чисел. Они обладают необычной историей, удивительными свойствами. 
Мы провели исследование среди 7, 8, 9 классов и выяснили, что многие ребята слышали об этих числах, но подробную информацию знают единицы. Многие из опрошенных учащихся хотели бы узнать об этих числах больше. 

Проблема: Многие дети считают математику скучной наукой сухих чисел. В связи с этим падает интерес к предмету, что отражается на результатах обучения.

Гипотеза: Если интересная информация о палиндромах, заинтересует школьников, то возможно они будут более углубленно изучать математику, что скажется на их математической грамотности и результативности обучения.

Разработанность исследуемой проблемы: Из современных палиндромистов наиболее известны В.Гершуни, Д.Авалиани, Б.Гольдштейн, Г.Лукомников (Бонифаций), А.Бубнов.

Цель: исследование палиндромов, репьюнитов, репдилжитов, выявление их особенностей и демонстрация возможности их использования на уроках математики и других предметов, расширение кругозора учащихся.

Для достижения цели нами перед нами были поставлены следующие задачи:

1. Изучить литературу по теме исследования: найти историю возникновения перевёртышей.

2. Рассмотреть свойства палиндромов, репдигитов и репьюнитов, установить связь между палиндромами, репьюнитами, репдигитами.

3. Выбрать предмет и продемонстрировать перевёртыши.

4. Составить свои перевёртыши (палиндромы), игры.

5. Предложить одноклассникам придумать свои перевёртыши (палиндромы), решить несколько задач олимпиадного типа по теме.

6. Сделать вывод.

Методы исследования:

• Теоретические: анализ, синтез, обобщение.

• Эмпирические: анкетирование, сравнение.

План исследования:

1. Выбор темы (октябрь 2017)

2. Изучение литературы по данной теме (ноябрь 2017)

3. Сбор информации (ноябрь 2017)

4. Проведение анкетирования (декабрь 2017)

5. Оформление работы (декабрь 2017 — январь 2018)

6. Защита работы (февраль 2018)

Знакомство с палиндромами.

Палиндро́м (от греч. πάλιν — ≪назад, снова≫ и греч. δρoμος—≪бег≫)

буквосочетание, слово или текст, одинаково читающиеся в обоих направлениях.[2]

Первые палиндромы появились в Древнем Риме, более 2000 лет тому назад. Ими украшали амфоры, чаши, вазы и другие предметы округлой формы. Такие надписи можно было читать в обе стороны, поворачивая сосуд в руках. Во фразах — палиндромах при чтении справа налево разорвутся слова, образуются новые, но порядок букв позволяет прочитать фразу и слева направо и справа налево.

Например: Мокнет Оксана с котенком.

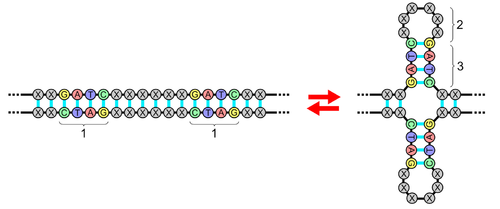
В истории человечества существуют примеры и несловесных палиндромов.[3]

А существуют ли палиндромы в математике?

Математические палиндромы обладают тем же свойством, т.е. число отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.

Числа — палиндромы образуют одно из наиболее интересных подмножеств множества натуральных чисел. Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо.

Например: 676; 9559; 1881; 74947; 7622267 и т. д.

Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром.
Например берем число 57:

1. 57+75=132

2. 132+231=363

Этим способом можно получить палиндром и из трехзначного числа.

Например, для числа 163:

1. 163+361 = 524

2. 524 + 425 = 949

А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Но есть числа, для которых этот способ «не работает». Известно, что выполняя сложение примерно десять миллионов раз, не удается превратить числа 196 или 879 в палиндромное. И до сих пор не найдено ни на каком шагу из этих чисел получится палиндром, ни строгого доказательства, что палиндром не будет получен никогда.

Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:

√ 484+³√ 1331=22+11=33

212²— 121²=44944-14641=30303

Некоторые свойства чисел-палиндромов.

До сих пор были рассмотрены в основном составные числа. Теперь обратимся к числам простым. В бесконечном множестве простых чисел имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11.

С такими числами связано немало интересных закономерностей:

• все однозначные числа являются палиндромами.

• существует единственный простой палиндром с чётным числом цифр –11.

• 26 – наименьшее число, не являющееся палиндромом, квадрат

которого палиндром. Например: 26² = 676

• 44562665878976437622437848976653870388884783662598425855963436955852489526638748888307835667984873422673467987856626544. Это число является в настоящее время мировым рекордом. Оно было найдено Джейсоном Дусеттом с помощью компьютера 30 ноября 2005 года.[4]

• первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5.

• среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1. Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.

• аналогичная картина наблюдается у больших простых чисел, например: 94849 и 94949; 1177711 и 1178711.

• пары чисел — ≪перевёртышей≫ 13 —31 и 113 —311 при возведении в квадрат дают также пары ≪перевёртышей≫: 169 —961 и 12769 —96721.Любопытно, что даже суммы их цифр оказались связаны хитрым образом:

(1 + 3)² = 1 + 6 + 9,

(1 + 1 + 3)² = 1 + 2 + 7 + 6 + 9.

Итак, палиндром— это число, которое одинаково читается слева направо и справа налево:

38683, 2002, 333, 11

Палиндром, составленный из одной и той же цифры, называют репди́гитом или репдиджитом (все репдигиты являются палиндромами и кратны репьюнитам):

7777

999

22

Многозначное натуральное число, составленное из одних единиц,называют репьюнитом:

11, 111, 1111

Между этими числами существует тесная связь, которую можно изобразить в виде схемы:

Удивительно то, что эта связь между числами проявляется и при выполнении арифметических операций.

Способ получения цепочки репдиджитов.

Число 111 111 111 делится на 9, так как сумма его цифр равна 9.Примечательно то, что в частном получается число 12345679:

111 111 111 = 9 ・ 12345679.

Отсюда можно получить пирамиду из девяти палиндромов — репдиджитов, умножая равенство сначала на 2, затем на 3, 4, …, 9:

1 ・ 9 ・ 12345679 = 111 111 111

2 ・ 9 ・ 12345679 = 222 222 222

3 ・ 9 ・ 12345679 = 333 333 333

…

9 ・ 9 ・ 12345679 = 999 999 999.

Возведение числа 11 в степень.

При возведении числа 11², 11³, 11⁴, …, я заметила закономерность:

11⁰ = 1

11¹ = 11

11² = 121

11³ = 1331

11⁴ = 14641

Оказывается, можно обойтись без умножения. Крайние цифры всех выписанных степеней – единицы, а чтобы получить остальные цифры каждого следующего числа, начиная с третьего, достаточно сложить две цифры предыдущего, стоящие над ним.

Продолжим поэтому правилу ≪пирамиду≫ степеней:

11⁵ = 161051

11⁶ = 1771561

11⁷ = 19487171

11⁸ = 214358881

11⁹ = 2357947691

11¹⁰ = 25934724601

11¹¹ = 285311670611 и т.д.

Возведение репьюнитов в квадрат.

Множество красивых чисел- палиндромов легко получить, возводяпервые девять репьюнитов в квадрат:

1² = 1

11² = 121

111² = 12321 и т.д.

111 111 111² = 12345678987654321

Так получается известный многим палиндром из единиц:

[5]

В этих палиндромах цифры в записи упорядочены сначала по возрастанию, а затем по убыванию. Добавление к записи репьюнита единицы увеличивает длину нового палиндрома на две цифры, при этом их общее количество остаётся нечётным. А вот центральная цифра n в числе 12…n…21 показывает, сколько единиц в породившем его репьюните.

Умножение репьюнитов разной длины.

Рассмотрим примеры:

11 ・ 111 = 1221

11 ・ 1111 = 12221

11 ・ 11111 = 122221

111 ・ 1111 = 123321

111 ・ 111111 = 12333321

Прослеживается закономерность: цифры в записи упорядочены сначала по возрастанию, а затем по убыванию, причём наибольшей цифрой является длина меньшего репьюнита, а количество повторений этой цифры в середине числа равно разности длин репьюнитов, увеличенной на единицу.

Например:

11…115 ・ 11…119 = 1234555554321

11…117 ・ 11…119 = 123456777654321

11…1113 ・ 11…116 = 123456666666654321.

Решение задач

1.Приведите пример числа-палиндрома, который делится на 15.

Решение: Число-палиндром – это число, которое остается неизменным, если его читать наоборот. Возьмем четырехзначное число-палиндром и составим его из цифр a и b, получим: abba. Нужно подобрать цифры a и b так, чтобы число abba делилось на 15, т.е. оно должно быть кратно 15. Чтобы число было кратно 15, цифра a должна быть равна 5. Остается подобрать цифру b так, чтобы число было кратно 15, получим:

— число 5115 – кратно 15;

— число 5225 – не кратно 15;

— число 5335 – не кратно 15;

— число 5445 – кратно 15; и т.д.

Ответ: 5115; 5445.

2.Найти все пары таких двузначных чисел, чтобы результат их сложения(вычитания, умножения, деления) не менялся в результате прочтения их суммы справа налево, т.е. х₁у₁+х₂у₂ = у₂х₂+у₁х₁

Решение:х₁у₁ = 10х₁ + у₁, х₂ у₂ = 10 х₂+у₂, тогда

(10х₁ + у₁) +(10х₂ + у₂ ) = (10у₂+х₂)+(10у₁+х₁).

Раскрыв скобки, приведя подобные слагаемые, разделив на 9, получим:х₁+х₂=у₁+у₂,

Вывод: сумма первых цифр у всех таких пар равна сумме их вторых цифр.

Примеры: 76+34=43+67 52+47 =74+25

3. Мири едет с папой в машине. В какой-то момент она посмотрела на счетчик километров и увидела число: 15951. «Папа, папа, смотри: это палиндромное число, учитель нам рассказывал о них!» Поездка оказалась продолжительной, и папа вел машину осторожно, с постоянной скоростью, а Мири поглядывала на счетчик. Через два часа на табло счетчика выскочило опять палиндромное число. С какой скоростью двигалась машина?

А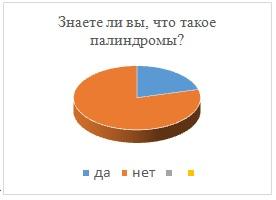нкетирование одноклассников:

В анкетировании приняло участие 24 человека. Им было предложено ответить на 3 вопроса:

Знаете ли вы что такое палиндромы? – нет-20

Встречались ли вы когда-нибудь с числами-палиндромами? — нет-21

Можете ли вы образовать число-палиндром? Если да, то образуйте одно число-палиндром? — нет-20

Результаты данного опроса изображены в виде секторной диаграммы, на основании которой можно сделать вывод о том, что о палиндромах знают только 5%. Среди опрошенных многие не знают, как образовать палиндром.

Задание для одноклассников: Я узнала, как можно получить такое число-перевёртыш.

Возьми любое число 619

Переверни его 916

Сложи два числа 1535

Переверни сумму 5351

Сложи два полученных числа 6886

Результат перевёртыш!

Оказывается, что все двузначные числа в конце концов дают палиндромы. Наибольшего числа шагов – по 24 – требуют числа 89 и 98.

Палиндромы могут стать предметом увлекательной коллективной игры.

• Участники должны написать в установленное время как можно больше чисел-палиндромов, слов-перевёртышей или фраз перевёртышей.

Результаты: Гипотеза подтвердилась.

• Изучили литературу по теме исследования: нашли историю возникновения перевёртышей

• Рассмотрели свойства палиндромов, репдигитов и репьюнитов, установить связь между палиндромами, репьюнитами, репдигитами

• Выбрали предмет и продемонстрировать перевёртыши в математике

• Составили свои перевёртыши (палиндромы), игры.

• Предложили одноклассникам придумать свои перевёртыши (палиндромы), решили несколько задач олимпиадного типа по теме

Выводы: Мир чисел настолько загадочен и увлекателен, что занимаясь данной работой, я поняла, если бы каждый из нас уделял ему больше внимания, то нашел бы для себя много нового и интересного. Я познакомилась с удивительными натуральными числами: палиндромами. Данная тема интересна одноклассникам, ее изучение можно продолжить в других предметах: ИЗО, окружающий мир, русский язык и другие.

В мире так много тайн и загадок, которые его украшают, и чудо палиндрома — это тоже одно из неповторимых таинств. Математики связывают с ним множество любопытных фактов и закономерностей: палиндромы делятся на пары и семейства, образуют числовые квадраты и целые симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр. В своей работе я показала, что нас окружают очень интересные вещи, но мы редко задумываемся об их происхождении и предназначении. Пусть эти числа еще не до конца изучены, и не ясно их применение, но может быть в результате таких опытов с числами, и откроется их истинная суть. А пока будем наслаждаться красотой чисел.

Перевёртыши на самом деле очень увлекательны, они помогают развивать интерес к познавательной деятельности. Я узнала, что палиндромы, это не только интересные картинки в изобразительном искусстве и окружающем мире, но и числа в математике, слова и фразы в русском языке. Мой кругозор стал шире, я узнала много интересной и полезной информации.

Я думаю, что моё исследование поможет улучшить память, мышление, воображение.

Думаю, что представленная мной работа будет весьма интересна и полезна ученикам, учителям и всем увлекающимся математикой людям.

Если Вас моя работа заинтересовала, её можно продолжить, найдя новые объекты исследования.

Список литературы:

1. http://www.nkj.ru/archive/articles/17984/ (Наука и жизнь№5,2010г).

2. Кацюба Е.А.Первый палиндромический словарь.— Москва, 1999.

3. Е.А.Новый палиндромический словарь.— Москва, 2002.

4. Федин С.Н. Палиндроматика // Математика для школьников. – 2005. — № 1, с. 54.

5. Кордемский Б.А. Удивительный мир чисел // книга для учащихся. – М.: Просвещение, 1995.

6. Кордемский Б. А.  На часок к семейке репьюнитов // Квант. -1997. — № 5. — с. 28-29.

7. Перельман Я.И. Занимательная математика // издательство «Тезис». – 1994

8. http://arbuz.uz/t_numbers.html

9. Журнал квант

10