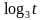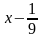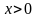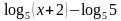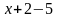Содержимое файла:
Тема урока. Метод рационализации в решении трансцендентных неравенств.
Цели урока:
Выработка творческого подхода к использованию теоретического материала вообще и свойств монотонных функции в частности.
Овладение новым методом решения трансцендентных неравенств.
Развитие навыков решения неравенств.
План урока:
Постановка цели урока.
Разбор домашнего задания и постановка проблемы.
Актуализация знаний.
Формулирование положений нового метода в процессе решения неравенства №1 (а) новым способом.
Решение неравенства №1(б) из домашней.
Самостоятельное (с обсуждением и корректировкой) решение неравенств.
Анализ домашнего задания (выявление проблем и предложения по их разрешению).
Итоги урока.
Дидактический материал (№№1-3 составлены автором, №4 из сборника: Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005):
В классе.
№1 а) 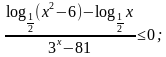 б)
б) 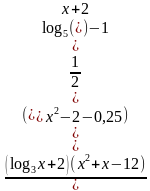 .
.
№2 а) 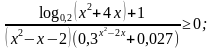 б)
б) 
Домашнее задание:
№3 а) 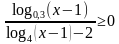 , б)
, б) 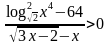 , в)
, в)  .
.
[№4] Функция  определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
 .
.
Ход урока.
|
Пункт плана |
учитель |
ученики |
интерактивная доска |
||||||||||||||||||||||||||||||||||||
|
2 |
Предлагает проверить №1(а) из домашней работы |
В основном справились, используя традиционный метод решения |
№1 (а)
|
||||||||||||||||||||||||||||||||||||
|
2 |
Предлагает проверить №1(б) из домашней работы |
В основном не справились, используя традиционный метод решения |
|
||||||||||||||||||||||||||||||||||||
|
2 |
Показывает равносильный переход в соответствии с традиционным методом решения. |
Сетуют на трудность и громоздкость решения и выражают надежду на возможность использования другого метода (формулируют проблему). |
№1 (б)
|
||||||||||||||||||||||||||||||||||||
|
3 |
Спрашивает: какие функции задействованы в обсуждаемых неравенствах? Что их объединяет? |
Называют функции и приходят к выводу, что все они монотонные. |
|
||||||||||||||||||||||||||||||||||||
|
3 |
Просит сформулировать определения возрастающей и убывающей функций. |
Приводят верные формулировки. |
Анимация: бегущий вверх (по графику) человечек
Опр.1: Функция
Анимация: бегущий вниз (по графику) человечек
Опр.2: Функция |
||||||||||||||||||||||||||||||||||||
|
4 |
Задаёт вопросы по заполнению ячеек таблицы (для анализа неравенства №1(а)) и заполняет её в соответствии с ответами детей. |
Отвечают на конкретные вопросы. |
|
||||||||||||||||||||||||||||||||||||
|
4 |
Предлагает осуществить равносильный переход в рамках рационализации неравенства. |
«Доброволец» записывает на ИД равносильное неравенство. |
|
||||||||||||||||||||||||||||||||||||
|
4 |
Предлагает учащимся самостоятельно закончить решение неравенства. Открывает окончание решения и ответ для проверки. |
Самостоятельно заканчивают решение неравенства в тетрадях. Проверяют это решение по образцу на ИД. |
Ответ.
|
||||||||||||||||||||||||||||||||||||
|
4 |
Предлагает учащимся сформулировать возникшие у них вопросы. Выносит на доску эти вопросы и предлагает желающим на них ответить. Предлагает вернутся к вопросам, на которые не нашлось ответа позже. |
Формулируют вопросы и отвечают на них. На основе этих ответов формулируются последующие вопросы, с ответами на которые возникают затруднения. |
Для каких неравенств применяется этот метод? + Что такое трансцендентное неравенство? + Почему этот метод называется «рационализация»? + В чём состоит эта рационализация? + Каковы рамки применения нового метода? + /- Обязательна ли разность функций? — Обязательна ли монотонность функций? — |
||||||||||||||||||||||||||||||||||||
|
5 |
Предлагает учащимся заполнить таблицу для анализа неравенства №1(б) |
Заполняют таблицу, используя раздаточный материал и проверят работу, выполненную на ИД (трое учащихся последовательно заполняют на ИД по одной строке в таблице). |
|
||||||||||||||||||||||||||||||||||||
|
5 |
Предлагает, используя таблицу, осуществить равносильный переход (рационализацию) и решить неравенство. |
Решают неравенство и проверяют решение, выполненное на обычной доске одним из учащихся. |
Ответ. |
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает для решения два неравенства. Спрашивает, какие трудности можно предвидеть. |
Формулируют проблемы. А) Не все множители являются разностями. Б) Не все функции монотонны. |
№2(б)
|
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает найти решение первой проблемы (вопрос 6) для неравенства №2(а): представить каждый из множителей в виде разноси монотонных функций. Спрашивает: можно ли представить в виде разности логарифмов сумму ? |
Отвечают, что можно и показывают как. |
|||||||||||||||||||||||||||||||||||||
|
6 |
Спрашивает: можно ли представить в виде разности сумму Возможно ли другое решение этой проблемы? |
Отвечают, что это невозможно и объясняют почему. Предлагают другое решение этой проблемы. |
|
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает самостоятельно решить неравенство №2(а), учитывая выработанные рекомендации. Через некоторое время открывает на ИД образец для проверки. |
Самостоятельно решают неравенство в тетрадях. |
№2(а) |
причём при |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
Ответ. |
|||||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает решить первую проблему для неравенства №2(б). |
Самостоятельно в тетрадях переписывают неравенство, представив каждый из множителей в виде разности, а один из учащихся делает это на ИД. |
.
|
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает решить вторую проблему (вопрос 7). Советует присмотреться к условиям, необходимым для решения неравенства. |
Замечают, что для решения неравенства необходимо выполнения условия |
Для существования решения неравенства необходимо выполнение условия |
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает самостоятельно решить неравенство №2(б), учитывая выработанные рекомендации. Через некоторое время открывает на ИД образец для проверки. |
Самостоятельно решают неравенство в тетрадях. |
Учитывая, что и получим Ответ. |
||||||||||||||||||||||||||||||||||||
|
6 |
Предлагает вернуться к вопросам 5). Каковы рамки применения нового метода? 6). Обязательна ли разность функций? 7). Обязательна ли монотонность функций? |
Формулируют четкие ответы на эти вопросы. |
|
||||||||||||||||||||||||||||||||||||
|
7 |
Предлагает проанализировать неравенства из №3 домашнего задания, представленного в раздаточных материалах и сформулировать проблемы, возникающие при их решении. Выражает уверенность в том, что задания из №3 будут успешно выполнены в ходе выполнения ДР, а также надежду, что и хитрое дополнительное задание (№4) также удастся решить. |
Формулируют проблему и намечают пути её решения. |
Как представить x в виде квадратного корня? Если Если Б) Как представить В) Как представить
|
||||||||||||||||||||||||||||||||||||
|
8 |
Предлагает оценить новый метод и перспективы его применения. |
Дают методу высокую оценку и предполагают, что он с успехом может быть применён при решении заданий №17 на ЕГЭ. |
|
||||||||||||||||||||||||||||||||||||
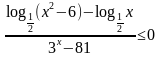


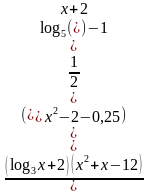 ?
?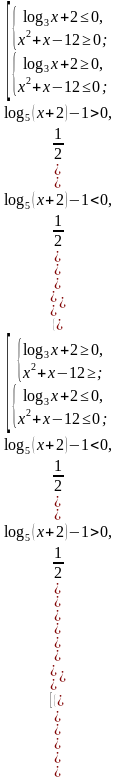
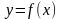 называется возрастающей, если для
называется возрастающей, если для  и
и 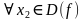 имеет место
имеет место 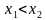

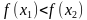 .
. .
.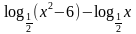
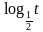
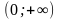
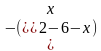

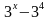
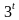
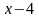
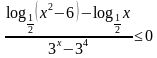
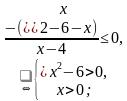
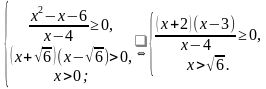
 ;3]
;3]